how to find equation of parabola with vertex and directrix

Parabola

A parabola is defined as a collection of points such that the altitude to a fixed bespeak (the focus) and a fixed direct line (the directrix) are equal. But it's probably easier to remember it every bit the U-shaped curved line created when a quadratic is graphed.

Many real-world objects travel in a parabolic shape. When yous shoot a basketball, the path of the ball creates a parabola.

Example

A parabola that is said to open upwards is shaped like a "U," while a parabola said to open downwards is shaped like an upside-downward U.

A parabola does not have to be vertical, but horizontal parabolas are not functions (they fail the vertical line test). Some functions you lot run across will be horizontal parabolas with restricted domains ( ). Y'all will learn more than about these when yous explore conics.

Example

The vertex of a parabola is the point where the parabola changes direction, and where the graph is most curved. On graphs of quadratics, it is found at the very top or lesser of the quadratic. The vertex is the point of the parabola at the axis of symmetry.

For quadratics in the standard course axⁱⁱ + bx + c, the axis of symmetry can be constitute using the equation 10 = . To find the y-coordinate of the vertex, find the centrality of symmetry and substitute that x-value into the original equation.

Example

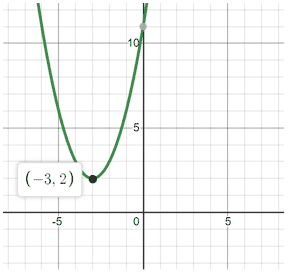
f(x) = x² + 6x + xi

a = ane; b = 6; c = xi

x = = -3

f(-iii) = (-3)² + 6(-3) + xi

f(-3) = nine - eighteen + 11 = 2

Vertex at (-three,2)

Calculating the focus and directrix

Below is an example of how to calculate the focus and directrix that may provide a meliorate understanding of the mathematical definition of a parabola provided above:

Example

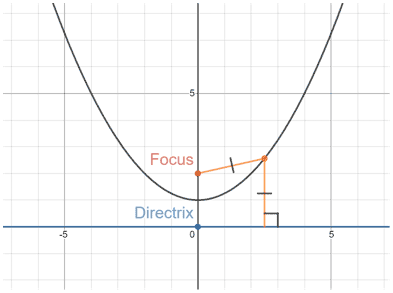
The focus is a indicate located on the same line as the axis of symmetry, while the directrix is a line perpendicular to the centrality of symmetry. For parabolas, the focus is ever on the within of the parabola, and the directrix never touches the parabola. Considering the vertex is the same distance from the focus and directrix, the directrix has a location straight contrary of the focus.

For a parabola in the vertex form y = a(x - h)² + k, the focus is located at (h, m + ) and the directrix is located at y = k - .

Example

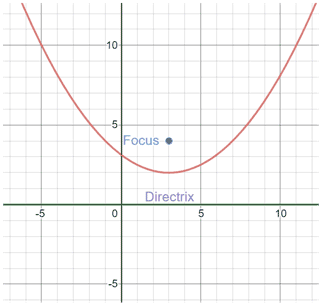
y = (x - 3)² + 2

h = 3 ; k = two ; a =

Focus: (3,ii + ) = (3,iv)

Directrix: y = 2 - = 0

For horizontal parabolas, the vertex is 10 = a(y - chiliad)^two + h, where (h,g) is the vertex. The focus of parabolas in this class have a focus located at (h + , yard) and a directrix at x = h - . The axis of symmetry is located at y = k.

Vertex class of a parabola

The vertex form of a parabola is another form of the quadratic function f(x) = ax² + bx + c. The vertex form of a parabola is:

f(x) = a(x - h)² + chiliad

The a in the vertex form of a parabola corresponds to the a in standard form. If a is positive, the parabola volition open upwards. If a is negative, the parabola will open downwardly.

In vertex form, (h,k) describes the vertex of the parabola and the parabola has a line of symmetry 10 = h.

Vertex form is very similar to the general expression for office transformations. Vertex course makes it much easier to graph a parabola considering it makes it easy to plot the vertex.

Instance

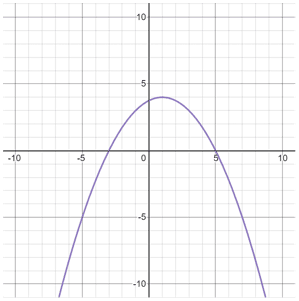
f(x) = -(x - i)ⁱⁱ + 4

From this equation, nosotros can already tell that the vertex of the parabola is at (1,4), and the axis of symmetry is at 10 = 1. At present all that has to exist done is to plug in points effectually the vertex, then graph.

Y'all can apply completing the square to convert a quadratic in standard form into vertex class. You can also convert to vertex course past using the knowledge that the vertex lies on the axis of symmetry.

The x-value of the vertex is x = - , so the y-value is y = f (- ). Plug these values in for h and k in the vertex form equation. And so, a is the same in both forms, so simply copy that to the vertex form equation.