how to find the vertex of a quadratic equation
VERTEX Grade OF A QUADRATIC EQUATION
Learning Objectives :
* Vertex form of a quadratic equation.
* If a quadratic equation is given in standard form, how to write information technology in vertex form.
* How to sketch the graph of a quadratic equation that is in vertex course.
Vertex form of a quadratic equation :
y = a(10 - h)2 + k
where (h, chiliad) is the vertex of the parabola.
The h represents the horizontal shift and k represents the vertical shift.
Horizontal Shift :
Shifting the graph of the parent function y = xiito the left or right from 10 = 0.
Vertical Shift :
Shifting the graph of the parent function y = x 2 upwards or down from x = 0.
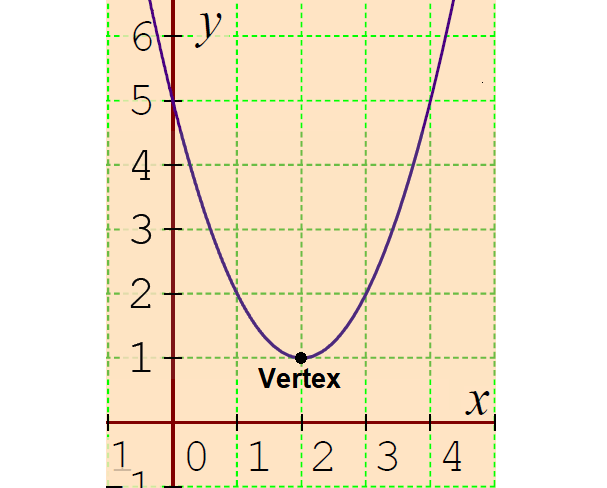
In the above picture, the graph (Parabola) of the parent part y = x2 is shifted ii units to the right from x = 0 and 1 unit up from y = 0.
So, the vertex is
(Horizontal shift, Vertical shift) = (ii, 1)
Example one :
Write the quadratic equation in vertex form and write its vertex :
y = -xii - 2x - 2
Solution :
Vertex form of the quadratic equation :
y = -x2 - 2x - ii
y = -(102 + 2x) - two
y = -[x2 + 2(x)(1) + 1two - 12] - 2
y = -[(x + one)2 - 12] - two
y = -[(x + 1)ii - 1] - 2
y = -(x + one)ii + 1 - ii
y = -(ten + 1)two - 1
Vertex :
Comparing y = a(x - h) ii + k and y = -(10 + 1) 2 - i,
h = -1 and k = -1
And then, the vertex is (h, k) = (-i, -one).
Example two :
Write the quadratic equation in vertex course and sketch the graph.
y = -ten2 + 2x + three
Solution :
Vertex class of the quadratic equation :
y = -tentwo + two10 + 3
y = -(xii - 2x) + iii
y = -[x2 - 2(x)(1) + 12 - oneii] + three
y = -[(x - 1)2 - 12] + 3
y = -[(x - 1)2 - i] + iii
y = -(x - 1)ii + ane + iii
y = -(x - 1)2 + 4
Vertex :
Comparingy = a(x - h) 2 + k and y = -(10 - 1) 2 + iv,
h = 1 and k = iv
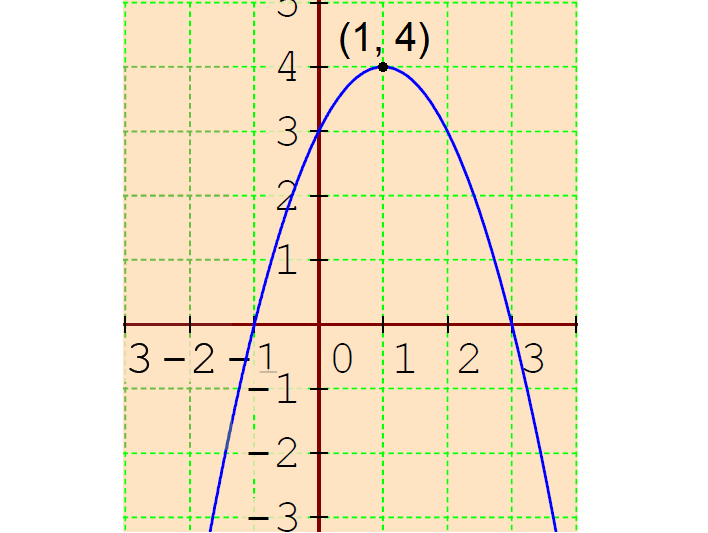
So, the vertex is (h, chiliad) = (1, 4).
To graph the above quadratic equation, we need to find 10-intercept and y-intercept, if whatsoever.
ten-intercept :
To find the x-intercept, substitute y = 0.
0 = -(x - ane)two + iv
(x - i)two = 4
Take square root on both sides.
x - 1 = ±√4
x - i = ±2
x - 1 = -two or x - 1 = 2
x = -1 or x = 3
So, the ten-intercepts are (-one, 0) and (iii, 0) .
y-intercept :
To find the y-intercept, substitute x = 0.
y = -(0 - ane)2 + 4
y = -(-1)2 + 4
y = -1 + iv
y = 3
And then, the y-intercept is (0, iii).
Comparingy = a(x - h) two + m and y = -(x - i) two + 4,
a = -one
So, the parabola opens down with vertex (1, 4), x-intercepts (-1, 0) and (iii, 0) and y-intercept (0, 3).
Kindly mail your feedback tov4formath@gmail.com
We e'er appreciate your feedback.
© All rights reserved. onlinemath4all.com
Source: https://www.onlinemath4all.com/vertex-form-of-a-quadratic-equation.html
Posted by: mccoyprideaught47.blogspot.com

0 Response to "how to find the vertex of a quadratic equation"
Post a Comment