How To Find The Roots Of A Polynomial Equation

Solving Polynomials

A polynomial looks like this:

example of a polynomial

Solving

"Solving" means finding the "roots" ...

... a "root" (or "naught") is where the function is equal to zero:

In between the roots the role is either entirely above,
or entirely below, the x-axis

Example: −2 and 2 are the roots of the function x² − four

Let's check:

• when x = −ii, then xⁱⁱ − 4 = (−2)ⁱⁱ − 4 = four − iv = 0
• when ten = two, and so x² − iv = ii² − 4 = 4 − 4 = 0

How practise we solve polynomials? That depends on the Caste!

Caste

The first stride in solving a polynomial is to observe its degree.

The Degree of a Polynomial with i variable is ...

... the largest exponent of that variable.

When we know the degree we can also requite the polynomial a name:

Caste	Proper noun	Example	Graph Looks Like
0	Constant	7
1	Linear	4x+3
2	Quadratic	xtwo−3x+2
iii	Cubic	2x3−5x2
4	Quartic	104+3x−ii	...
etc	...	...	...

How To Solve

And then now we know the degree, how to solve?

• Read how to solve Linear Polynomials (Degree ane) using elementary algebra.
• Read how to solve Quadratic Polynomials (Caste 2) with a piffling piece of work,
• It can be difficult to solve Cubic (degree 3) and Quartic (caste 4) equations,
• And beyond that it tin can be incommunicable to solve polynomials directly.

So what do we do with ones we can't solve? Try to solve them a piece at a time!

If we find one root, we can and so reduce the polynomial by one degree (example later) and this may be enough to solve the whole polynomial.

Hither are some main means to find roots.

ane. Basic Algebra

We may be able to solve using bones algebra:

Example: 2x+1

2x+1 is a linear polynomial:

The graph of y = 2x+i is a straight line

It is linear so in that location is one root.

Use Algebra to solve:

A "root" is when y is zero: 2x+one = 0

Subtract i from both sides: 2x = −ane

Dissever both sides by 2: 10 = −1/ii

And that is the solution:

x = −1/ii

(You can besides see this on the graph)

Nosotros can also solve Quadratic Polynomials using basic algebra (read that folio for an explanation).

2. By experience, or but guesswork.

It is ever a proficient idea to come across if we tin do simple factoring:

Example: 10ⁱⁱⁱ+2xⁱⁱ−x

This is cubic ... only wait ... we can cistron out "x":

ten³+2x^two−x = ten(x²+2x−1)

At present we take 1 root (x=0) and what is left is quadratic, which nosotros can solve exactly.

Or we may detect a familiar pattern:

Example: x³−8

Again this is cubic ... but it is also the "divergence of ii cubes":

10³−8 = ten³−2ⁱⁱⁱ

And so nosotros can turn it into this:

10³−eight = (x−ii)(10^two+2x+4)

In that location is a root at x=ii, because:

(2−two)(2^two+2×2+4) = (0)(2²+2×2+four)

And nosotros can and so solve the quadratic x²+2x+4 and we are washed

3. Graphically.

Graph the polynomial and see where it crosses the x-centrality.

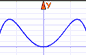We tin enter the polynomial into the Part Grapher, and then zoom in to find where it crosses the ten-centrality.

Graphing is a skillful mode to notice estimate answers, and nosotros may too get lucky and detect an verbal reply.

Circumspection: earlier y'all jump in and graph it, you should really know How Polynomials Conduct, so you discover all the possible answers!

Factors

This is useful to know: When a polynomial is factored like this:

f(x) = (x−a)(x−b)(10−c)...

Then a, b, c, etc are the roots!

Then Linear Factors and Roots are related, know ane and nosotros can find the other.

(Read The Factor Theorem for more details.)

Example: f(10) = (tenⁱⁱⁱ+2x²)(x−3)

Nosotros see "(x−3)", and that means that 3 is a root (or "zilch") of the function.

Sure?

Well, let united states of america put "3" in place of x:

f(ten) = (iii³+2·three²)(3−3)

f(iii) = (3³+2·3ⁱⁱ)(0)

Yep! f(iii)=0, so iii is a root.

How to Cheque

Constitute a root? Check it!

Simply put the root in place of "x": the polynomial should be equal to goose egg.

Example: 2x³−x²−7x+2

The polynomial is degree iii, and could be hard to solve. So let us plot it first:

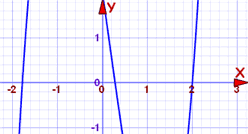
The curve crosses the x-axis at three points, and one of them might be at 2. Nosotros tin cheque easily, just put "2" in place of "x":

f(two) = 2(2)³−(ii)ⁱⁱ−seven(ii)+2
= 16−4−14+2
= 0

Yes! f(2)=0, and then we accept constitute a root!

How well-nigh where it crosses near −one.8:

f(−ane.eight) = ii(−ane.8)³−(−ane.eight)^two−seven(−1.viii)+2
= −11.664−3.24+12.6+2
= −0.304

No, information technology isn't equal to nada, so −one.8 will not be a root (but information technology may exist close!)

Only we did discover one root, and nosotros can use that to simplify the polynomial, like this

Instance (continued): 2x³−xⁱⁱ−7x+ii

And then, f(2)=0 is a root ... that means we as well know a gene:

(ten−2) must exist a factor of 2x³−x²−7x+2

Next, divide 2x³−ten²−7x+2 past (10−ii) using Polynomial Long Partitioning to find:

2x³−x²−7x+2 = (x−2)(2xⁱⁱ+3x−ane)

So now we can solve 2x²+3x−1 as a Quadratic Equation and nosotros will know all the roots.

That final example showed how useful it is to discover just one root. Retrieve:

If nosotros find i root, we tin can and so reduce the polynomial past one degree and this may be enough to solve the whole polynomial.

How Far Left or Right

When trying to detect roots, how far left and right of zip should nosotros go?

In that location is a way to tell, and there are a few calculations to do, but it is all simple arithmetic. Read Bounds on Zeros for all the details.

Take We Got All The Roots?

In that location is an easy manner to know how many roots there are. The Cardinal Theorem of Algebra says:

A polynomial of degree n ...
... has n roots (zeros)
simply we may need to use complex numbers

So: number of roots = the degree of polynomial.

Example: 2x³ + 3x − 6

The degree is 3 (because the largest exponent is 3), and and so:

There are iii roots.

But Some Roots May Be Complex

Yes, indeed, some roots may be complex numbers (ie have an imaginary part), and so will not show upwards as a simple "crossing of the x-axis" on a graph.

Only there is an interesting fact:

Circuitous Roots always come in pairs!

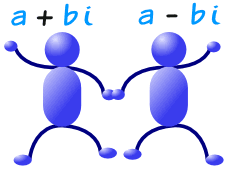
Then we either go no circuitous roots, or 2 circuitous roots, or 4, etc... Never an odd number.

Which means we automatically know this:

Degree	Roots	Possible Combinations
1	1	1 Real Root
2	two	ii Existent Roots, or ii Complex Roots
three	3	3 Real Roots, or 1 Real and 2 Complex Roots
4	4	4 Real Roots, or 2 Real and 2 Circuitous Roots, or iv Complex Roots
etc		etc!

Positive or Negative Roots?

There is likewise a special fashion to tell how many of the roots are negative or positive called the Rule of Signs that you lot may like to read about.

Multiplicity of a Root

Sometimes a factor appears more once. Nosotros call that Multiplicity:

Multiplicity is how often a certain root is part of the factoring.

Example: f(x) = (x−5)³(x+7)(x−i)²

This could be written out in a more lengthy manner similar this:

f(x) = (x−5)(ten−v)(x−5)(x+vii)(x−1)(ten−1)

(x−five) is used iii times, so the root "5" has a multiplicity of 3, likewise (x+seven) appears once and (x−1) appears twice. So:

• the root +5 has a multiplicity of 3
• the root −7 has a multiplicity of i (a "simple" root)
• the root +i has a multiplicity of 2

Q: Why is this useful?
A: Information technology makes the graph behave in a special manner!

When we see a factor like (x-r)ⁿ , "northward" is the multiplicity, and

• even multiplicity just touches the axis at "r" (and otherwise stays one side of the x-axis)
• odd multiplicity crosses the axis at "r" (changes from 1 side of the x-axis to the other)

We tin run across it on this graph:

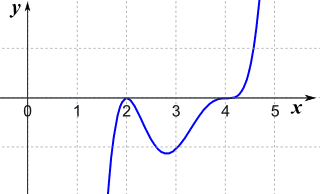
Example: f(x) = (10−two)²(x−4)³

(x−two) has fifty-fifty multiplicity, then it just touches the axis at ten=2

(x−4) has odd multiplicity, and so it crosses the centrality at x=4

Similar this:

Summary

Nosotros can direct solve polynomials of Degree 1 (linear) and 2 (quadratic)
For Caste 3 and up, graphs tin be helpful
It is also helpful to:
• Know how far left or right the roots may exist
• Know how many roots (the same as its degree)
• Estimate how many may be complex, positive or negative
Multiplicity is how often a certain root is role of the factoring.

Source: https://www.mathsisfun.com/algebra/polynomials-solving.html

Posted by: mccoyprideaught47.blogspot.com

Share this post